Understanding Simpson’s Paradox: A Simple Explanation

rstats
modeling
Published

January 12, 2024

Simpson's Paradox is a statistical phenomenon where a trend appears in different groups of data but disappears or reverses when these groups are combined. This paradox highlights the importance of considering confounding variables and understanding the causal relationship between variables.

Example Scenario: Work Environment

Let’s consider a hypothetical work environment where the number of women (W) is greater than the number of men (M). However, when looking at the distribution of managerial positions (P), it seems that more men occupy higher-level positions compared to women.

Now, suppose there’s a characteristic Z, representing gender, and you suspect it might influence the choice of assigning a managerial position (P) because a specific time dedicated to a critical task (T) is primarily marketed toward men (M).

To illustrate this paradox, we’ll create synthetic data in R.

Install and load necessary library

Set seed for reproducibility

Generate synthetic data

n <- 1000  # Number of employees 
W <- round(runif(n, 200, 800))  # Number of women
M <- n - W  # Number of men

Assign managerial positions based on gender and a confounding variable

P_W <- round(runif(W, 0, 1))  # 0 for no managerial position, 1 for managerial position for women
P_M <- round(runif(M, 0.2, 1))  # Higher chance of managerial position for men due to confounding variable

Create a data frame

w <- tibble(gender="Women",count=W,manager=P_W)

m <- tibble(gender="Men",count=M,manager=P_M)

data <- rbind(w,m)
data%>%head
# A tibble: 6 × 3
  gender count manager
  <chr>  <dbl>   <dbl>
1 Women    373       0
2 Women    673       1
3 Women    445       0
4 Women    730       1
5 Women    764       1
6 Women    227       0

Display the initial summary

summary(data)
    gender              count        manager      
 Length:2000        Min.   :200   Min.   :0.0000  
 Class :character   1st Qu.:352   1st Qu.:0.0000  
 Mode  :character   Median :500   Median :1.0000  
                    Mean   :500   Mean   :0.5615  
                    3rd Qu.:648   3rd Qu.:1.0000  
                    Max.   :800   Max.   :1.0000

In this example, we have created a dataset with a larger number of women, but the chance of obtaining a managerial position for men is influenced by a confounding variable. Now, let’s examine the paradox.

Calculate the proportion of managerial positions for each gender

proportion_table <- data %>%
  group_by(gender) %>%
  summarize(proportion = mean(manager))

Display the proportions

proportion_table
# A tibble: 2 × 2
  gender proportion
  <chr>       <dbl>
1 Men         0.626
2 Women       0.497
library(ggplot2)
proportion_table%>%
  ggplot(aes(gender,proportion,fill=gender))+
  geom_col(color="white",show.legend = F)+
  scale_fill_viridis_d()+
  labs(title = "Proportion of Managers by Gender",
       subtitle = "Example of the Simpson's Paradox",
       x="",
       caption = "Data: Syntetic | Graphics: Federica Gazzelloni") +
  coord_equal()+
  ggthemes::theme_pander()+
  theme(plot.caption = element_text(hjust = 0.5))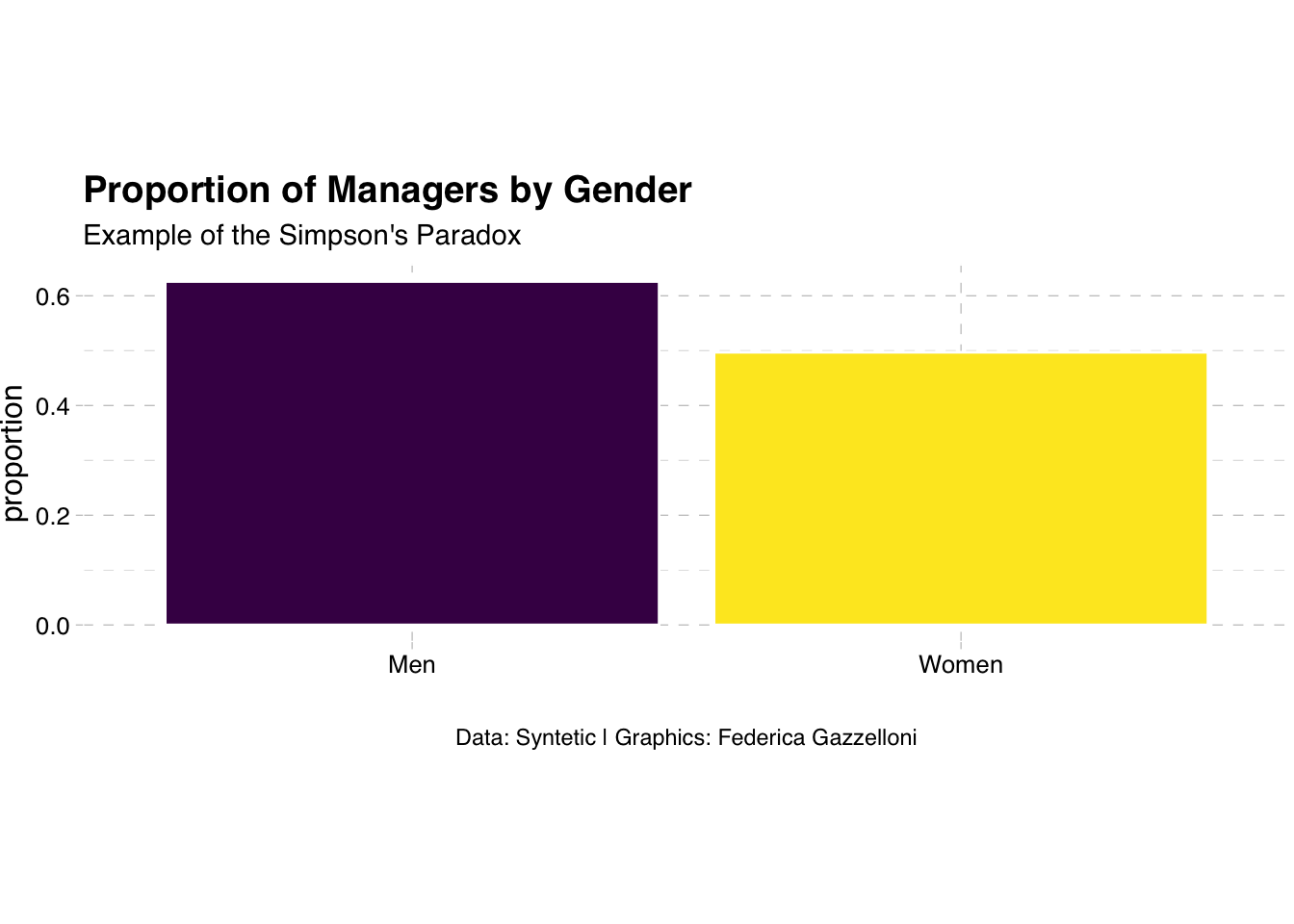

In this scenario, when examining the proportion of managerial positions within each gender group, it might appear that men have a higher chance. However, when we consider the entire dataset, we may find the opposite due to the confounding variable.

The key takeaway is that understanding causation is crucial, and Simpson’s Paradox emphasizes the need to consider confounding factors when interpreting data.

Back to top